Burkay T. Öztürk, University of Illinois at Chicago
1. Introduction
Formalists of the early 20th century such as David Hilbert hoped to construct formal deductive systems where one can express and prove all truths of pure mathematics by manipulating a set of axioms according to logically sound inference rules. Gödel’s First Incompleteness Theorem showed that for any formal system capable of expressing such truths, some mathematical truths will not be provable in the system.
In his paper “On Formally Undecidable Propositions of Principia Mathematica and Related Systems I” Gödel makes the following observation:
The development of mathematics towards greater exactness has, as is well-known, lead to
formalization of large areas of it such that you can carry out proofs by following a few
mechanical rules. The most comprehensive current formal systems are the system of Principia
Mathematica (PM) on the one hand, the Zermelo-Fraenkelian axiom-system of set theory on
the other hand. These two systems are so far developed that you can formalize in them all
proof methods that are currently in use in mathematics, i.e. you can reduce these proof
methods to a few axioms and deduction rules. Therefore, the conclusion seems plausible
that these deduction rules are sufficient to decide all mathematical questions 1 expressible in those systems 2
As Gödel went on to prove in the same paper, this seemingly plausible conclusion is false. Russell and Whitehead’s Principia Mathematica (henceforth, PM) and similar endeavors are all destined to fail in attaining provability of all mathematical truths. However, in retrospect PM also appears to have a problem concerning expressibility of mathematical propositions. Although this problem is not as spectacular as that was uncovered by Gödel, it still raises the question if PM as a formal system was even less well-suited for the formalistic project than it seemed.
In this paper, I deploy a diagonal argument to the effect that PM as a formal system has a problem with expressing all mathematical content there is to express. However, this negative result raises another question, a strictly historical one: How did Russell, who proved Frege’s Grundlage inconsistent by using a diagonal argument, not see this coming? I think the answer to this historical question lies in the nuances of Russell’s ideas about what logic is and the relationship between logic and PM.
2. Propositional Functions and Expressibility in PM
In PM, Russell and Whitehead used sets to define mathematical entities and prove theorems about them. However, sets themselves were not primitives. Sets, ordinary mathematical functions and even truth functional operators were defined in terms of what they called “propositional functions.” In this regard, expressibility in PM boils down to the expressive power of propositional functions.
A propositional function is a statement containing one or more free variables, which yields a proposition when those variables are substituted 3 with the names of things. For instance, “x is a prime number” is a propositional function, which yields a true proposition when the free variable x is substituted with 17 and yields a false proposition when substituted with 16. Similarly, “It is the case that p and q,” which is the truth functional operator which we today call “conjunction,” is a propositional function with two free variables. If and only if p and q are substituted with true propositions the function yields a true proposition. Now, we have the conceptual tools necessary for discussing the problems concerning the expressibility in PM.
The language of PM is finitary, which means that there are denumerably many symbols in it. So, there are at most denumerably many propositional functions with one free variable. Let ψ1x, ψ2x, … be the list of those propositional functions. Now, consider the following table:
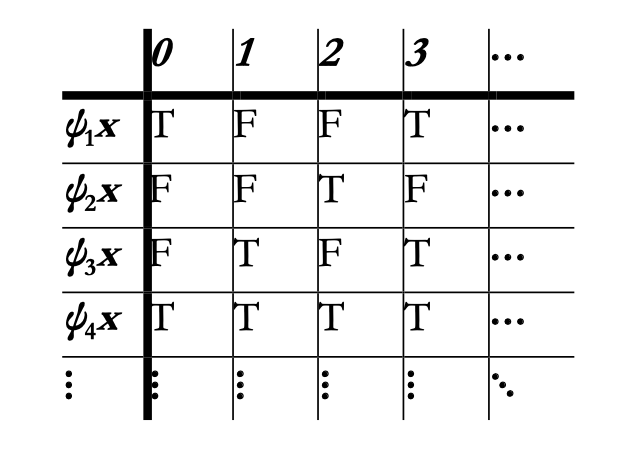
In the table, the left-hand side column is an exhaustive enumeration of all propositional functions
with exactly one free variable. 4 The top row is an exhaustive enumeration of all numerals, which are
the names of natural numbers. Each row of the table contains – or would contain if we were to
spend an eternity filling them out – the truth values of the propositions acquired by substituting the numerals in for x in the function on that row. For instance, the first line contains the following information: Substituting in 0 for x in ψ1x gives us a true proposition, substituting in 1 for x in ψ1x gives us a false proposition, substituting in 2 for x in ψ1x gives us a false proposition, substituting 3 for x in ψ1x gives us a true proposition, and so on.
To get a clear sense of what the table is about consider the following illustration: Suppose ψ1x is the propositional function “x is divisible by 3.” It expresses a true proposition if you substitute x with the numerals 0 or 3, but expresses a false proposition if you substitute it with the numerals 1 or 2. This is so because 0 and 3 are divisible by 3 whereas 1 and 2 are not.
In this regard, each row of the table consists of the truth value content of a propositional function in PM. Let’s call these rows “truth sequences.” A truth sequence consists of denumerably many ordered spots. For instance, the truth sequence corresponding to ψ1x has a T in its first spot, Fs in its second and third spots, a T in its fourth spot, and so on. Let S be the set of all possible truth sequences.
By using a diagonal argument, we shall now prove that there are more truth sequences in S than there are propositional functions in PM. Let’s focus on the diagonal of the table:
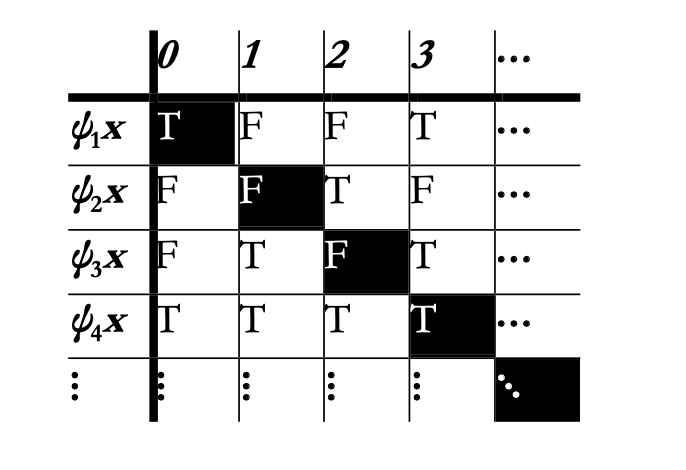
The diagonal itself is a truth sequence, which has a T in its first spot, Fs in its second and third spots, a T in its fourth spot and so on.
Now, let’s define a function f : S➝S such that for a truth sequence s and for all values of n, if the nth spot ofs is occupied by a T, the nth spot off(s) is occupied by an F and ifthe nth spot ofs is occupied by an F, the nth spot of f(s) is occupied by a T.
In less formal terms, f inverts all the truth values in a given truth sequence. For instance, if you apply it to the truth sequence contained in the diagonal, you get (F, T, T, F, …). Let’s call this anti-diagonal sequence α.
The anti-diagonal sequence α is not contained in the table as a row because by the definition of f, α is guaranteed to be different from all rows of the table at least in one spot. More precisely, α is
guaranteed to be different from the nth truth sequence in the table at least in the nth spot. Since α itself is a truth sequence, there are possible truth sequences that do not have corresponding propositional functions in PM.
As in the other diagonal arguments such as Cantor’s proof that there are more reals in a
finite interval than all natural numbers, inserting α into the table by making up a new propositional
function is no solution. Such an insertion will create a new table and there will be a new diagonal for
which f will produce a new truth sequence that is not contained in the new table. In other words,
whatever the propositional functions of PM are, there are truth sequences that do not correspond to any of them. 5
3. Interpretation of the Result
So far we have demonstrated that for PM and similar formal systems, there will be truth sequences that fall beyond the expressive power of the system. However, as with most technical results, it is not self-evident what the philosophical significance of the demonstration is, or even if it is significant at all. Before arguing that the result at hand has philosophical and historical significance, I will make two disclaimers.
First, it is important to notice that we have not demonstrated that there are mathematical propositions which PM cannot express, at least in Russell’s sense of propositions. On Russell’s account, propositions are neither truth sequences nor spots in them. For Russell, propositions are abstract composits consisting of objects and universals. For example, the proposition expressed by “Socrates is mortal” consists of Socrates-the-man and the universal mortal. In this regard, perhaps Russell would not have been shaken by our argument.
Moreover, there is a distinct sense in which systems like PM are expressively complete for practical intents and purposes. If they were not complete, mathematicians and mathematical logicians would have noticed and complained, wouldn’t they?
Contrary to the intuitions expressed above I think we have an interesting negative result concerning the expressive limitations of PM and similar formal systems in our hands. To see this, consider the original list of propositional functions that we attributed to PM. For the sake of illustration, we identified ψ1x as the propositional function “x is divisible by 3.” We can extend this identification, and assign a distinct mathematical meaning to each row in the table. For instance, ψ4x could be “x is less than 155065.”
Now think about α, which does not correspond to any propositional function in PM. What is the mathematical meaning associated with it? Claiming, without argument, that there is no such meaning would be ad hoc. After all, there is an extension of PM where there is a propositional any of them function ψαx which corresponds to α, and it yields a true proposition when we substitute 1 in for x inside ψαx. If α had no mathematical meaning associated with it, then how it could express a true proposition about number 1?
This also explains why mathematicians and mathematical logicians would never complain about the sort of inexpressibility in question. Any time you have a mathematical proposition that is not expressible in the system you work with, you can extend your formal system by inserting a new propositional function. Therefore, unless you are looking for a proof of expressive completeness, you would never notice that it is not there. This may sound odd, but the situation is perfectly familiar. Think of Cantor’s diagonal argument for the fact that real numbers outstrip the naturals: Any time you find a real that your supposed one-to-one mapping does not cover, you can shift your original map by one natural and make space for the unmapped real. The problem is that the new list leaves some other real numbers unmapped, which you would never notice unless you see the reasoning involved in the diagonal argument.
So we have reason to think that PM as a formal system falls short not only in deciding the truth value of all mathematical propositions as Gödel proved, but also in expressing all mathematical content there is to express.
But isn’t this historically odd? Certainly Russell wasn’t a novice about diagonal arguments. As Russell admits, his celebrated paradox, which exploits Frege’s Rule V, was produced after a close study of Cantor’s proof for his famous theorem, which employs the diagonal argument, and the paradox itself is an elegant case of the diagonal argument.
Cantor had a proof that there is no greatest cardinal; in applying this proof to the universal class, I was led to the contradiction about classes that are not members of themselves. It soon became clear that this is only one of an infinite class of contradictions. I wrote to Frege, who replied with the utmost gravity that “die Arithmetik ist ins Schwanken geraten.” 6
In this regard, it would be naive to believe that Russell simply failed to notice the diagonal argument that I provided above.
It seems that we have managed to transform a technical result into a historical puzzle: How do we explain the limits of expressibility in PM as a formal system in a way that respects Russell’s mastery over diagonal arguments? As I will show below, solving this historical puzzle demands an appreciation of Russell’s views about the status of logic and its relationship to PM construed as a formal system.
4. A Historical Resolution
Although certain similarities between Russell’s and Hilbert’s views may create the opposite impression, Russell never endorsed the formalist program. The following is an excerpt from Russell’s My Philosophical Development: “The primary aim of Principia Mathematica was to show that all pure mathematics follows from purely logical premisses and uses only concepts definable in logical terms.” 7
Hilbert’s “Foundations of Mathematics” opens with deceptively similar prose:
I pursue a significant goal, for I should like to eliminate once and for all the questions regarding the foundations of mathematics, in the form in which they are now posed, by turning every mathematical proposition into a formula that can be concretely exhibited and strictly derived, thus recasting mathematical definitions and inferences in such a way that they are unshakeable and yet provide an adequate picture of the whole science. I believe that I can attain this goal completely with my proof theory. 8
However, the similarity is only superficial. In addition to the fact that Hilbert did not like Russell’s axioms of infinity and reducibility, there were also very decisive “philosophical” differences between Russell’s logicistic outlook and Hilbert’s formalist program. One such crucial difference for our purposes is best expressed in the following excerpts, again one from Russell and one from Hilbert:
Some indemonstrables there must be; and some propositions, such as the syllogism, must be of the number, since no demonstration is possible without them. But concerning others, it may be doubted whether they are indemonstrable or merely undemonstrated; and it should be observed that the method of supposing an axiom false, and deducing the consequences of this assumption, which has been found admirable in such cases as the axiom of parallels, is here not universally available. For all our axioms are principles of deduction; and if they are true, the consequences which appear to follow from the employment of an opposite principle will not really follow. 9
So, for Russell formal systems are meant to mirror logic, which is the body of truths about what
follows from what. On this view, axioms of logic are nothing but the fundamental laws of reasoning.
If any of the assumptions one makes when constructing or inspecting a formal system contradicts an
axiom of logic, what formally “follows” from that assumption in that system is inevitably non
sequitur. 10 ThisiswhythefailureofoneformalsystemsuchasPM–orallformalsystemsasfaras
I can attain this goal completely with my proof theory.
principle will not really follow
Russell would be concerned – to prove or even express all mathematical truths is at most a failure to attain the “primary aim” Russell had in mind when co-writing PM, not a refutation of logicism. Russell’s logicism was the thesis that logic is a body of truths. The borders of this body may either overlap with or outstrip the limits of formal systems. What mattered for him was that all pure mathematics follows from these truths demonstrably or not. Gödel showed that for no formal system such a demonstration is possible for every truth. Although this raises doubts about the possibility of any positive argument for logicism, it is not a refutation of logicism itself.
However, Hilbert’s bet was on a different horse. In his “Foundations of Mathematics” Hilbert argued:
No more than any other science can mathematics be founded by logic alone; rather, as a condition for the use of logical inferences and the performance of logical operations, something must already be given to us in our faculty of representation, certain extra-logical concrete objects that are intuitively present as immediate experience prior to in thought. If logical inference is to be reliable, it must be possible to survey these objects completely in all their parts, and the fact that they occur, that they differ from one another, and that they follow each other, or are concatenated, is immediate, given intuitively, together with the objects, is something that neither can be reduced to anything else nor requires reduction. This is the basic philosophical position that I regard as requisite for mathematics and, in general, for all scientific thinking, understanding, and communication. And in mathematics, in particular, we consider is the concrete signs themselves, whose shape, according to the conception we have adopted, is immediately, clear and recognisable. This is the very least that must be presupposed; no scientific thinker can dispense with it, and therefore everyone must maintain it, consciously, or not. 11
In this regard, Hilbert’s formalism was the following thesis: One can construct a formal system which allowed for the demonstration of all truths of pure mathematics by manipulating extra-logical concrete objects (i.e., mathematical signs on paper) in a way that conforms to the logical rules of inference. This is why Gödel’s first theorem (i.e., the fact that in every formal system there will be some mathematical truths that elude such demonstration) is a refutation of Hilbert’s formalism.
The highlighted contrast between Russell’s logicism and Hilbert’s formalism culminates to a solution to our historical puzzle. As pointed out earlier, propositional functions are the building blocks of PM. When we treat PM as a formal system, propositional functions end up being pieces of a language, strings of symbols containing variables to be substituted with the names of individual objects. Only when propositional functions are strings of symbols the diagonal argument works.
must maintain it, consciously, or not.
Taking seriously Russell’s belief (i.e., the belief that logic is not a formal system) undercuts the perceived expressive inadequacy. If propositional functions are not linguistic objects, then there is no reason to think that there will be denumerably many of them. In other words, the perceived expressive inadequacy comes up only when one hijacks Russell’s ideas and tries to apply them in a decidedly formalist framework.
Bibliography
Gödel, Kurt. Collected Works Vol. 1. Eds. S. Feferman, et al. Oxford: Oxford UP, 1986.
Gödel, Kurt. “Über formal unentscheidbare Sätze der Principia mathematica und verwandter Systeme
I.” Monatshefte für Mathematik und Physik 38 (1931): 173-198.
Hilbert, David. “Foundations of Mathematics.” In The Emergence of Logical Empiricism. Ed. S. Sarkar.
New York: Garland Publishing Inc., 1996. 228-243.
Hylton, Peter. Propositions, Functions, and Analysis: Selected Essays on Russell’s Philosophy. New York: Oxford UP, 2005.
Russell, Bertrand. “My Mental Development.” In The Basic Writings of Bertrand Russell. Eds. R. E. Egner and L. E. Denonn. New York: Routledge, 1961. 9-22.
Russell, Bertrand. My Philosophical Development. New York: Routledge, 1954.
Russell, Bertrand. Principles of Mathematics. Cambridge: Cambridge UP, 1903.
Russell, Bertrand and Alfred North Whitehead. Principia Mathematica. 2nd Ed. Cambridge: Cambridge UP, 1927.
- We can treat “questions” as synonymous with “propositions” in this context. After all, mathematicians decide mathematical questions by determining the truth values of mathematical propositions.
- Kurt Gödel, “Über formal unentscheidbare Sätze der Principia mathematica und verwandter Systeme I,” Monatshefte für Mathematik und Physik 38 (1931): 173-174. For a relatively recent English translation of the entire text, see Kurt Gödel, “On Formally Undecidable Propositions of Principia Mathematica and Related Systems I,” in Collected Works Vol. 1, edited by S. Feferman, et al. (Oxford: Oxford UP, 1986) 144–195.
- By the time of PM’s publication, Russell held a view which he dubbed “the theory of substitutions” about what exactly is being substituted in and out. The theory claimed that the substituted things are not names of objects, but objects themselves. For example, when you take the propositional function “x is mortal,” and substitute in Socrates for x to get the proposition expressed by “Socrates is mortal,” you are substituting Socrates-the-man for x, not “Socrates”-the-name. It is not clear how exactly this bizarre theory was supposed to work, but Russell later abandoned it in favor of the substitution involving names and justified his change of heart by appealing to the technical inconvenience of his former view.
- The same argument can be extended easily to the propositional functions that admit more than one variable using tables with more than two dimensions.
- On one occasion, Russell comes very close to this particular result. In Principles of Mathematics (Cambridge: Cambridge UP, 1903), he observes:
We can easily prove that there are more propositional functions than objects. For suppose a correlation of all objects and some propositional functions to have been affected, and let φx be the correlate of x. Then “not-φx(x)”, i.e. “φx does not hold of x”, is a propositional function not contained in the correlation; for it is true or false of x according as φx is false or true of x, and therefore it differs from φx for every value of x. (372) Russell here argues that there are more propositional functions than objects. The result concerning the perceived inadequacy is that there is more mathematical content than there are propositional functions. Therefore, even though Russell’s observation is correct, it is not quite the same as the result we have in our hands.
- Bertrand Russell, “My Mental Development,” in The Basic Writings of Bertrand Russell, edited by R. E. Egner and L. E. Denonn (New York: Routledge, 1961) 16, emphasis mine.
- Bertrand Russell, My Philosophical Development (New York: Routledge, 1954) 57.
- David Hilbert, “Foundations of Mathematics,” in The Emergence of Logical Empiricism, edited by S. Sarkar (New York: Garland Publishing Inc., 1996) 228.
- Russell, Principles of Mathematics, 15.
- I would like to thank Professor Peter Hylton for bringing this aspect of Russell’s logicism to my attention. For an article-length treatment of Russell’s notion of logic see “Logic in Russell’s Logicism” by Hylton, published in his Propositions, Functions, and Analysis: Selected Essays on Russell’s Philosophy (New York: Oxford UP, 2005) 49-83.
- David Hilbert, “Foundations of Mathematics,” 228-229.